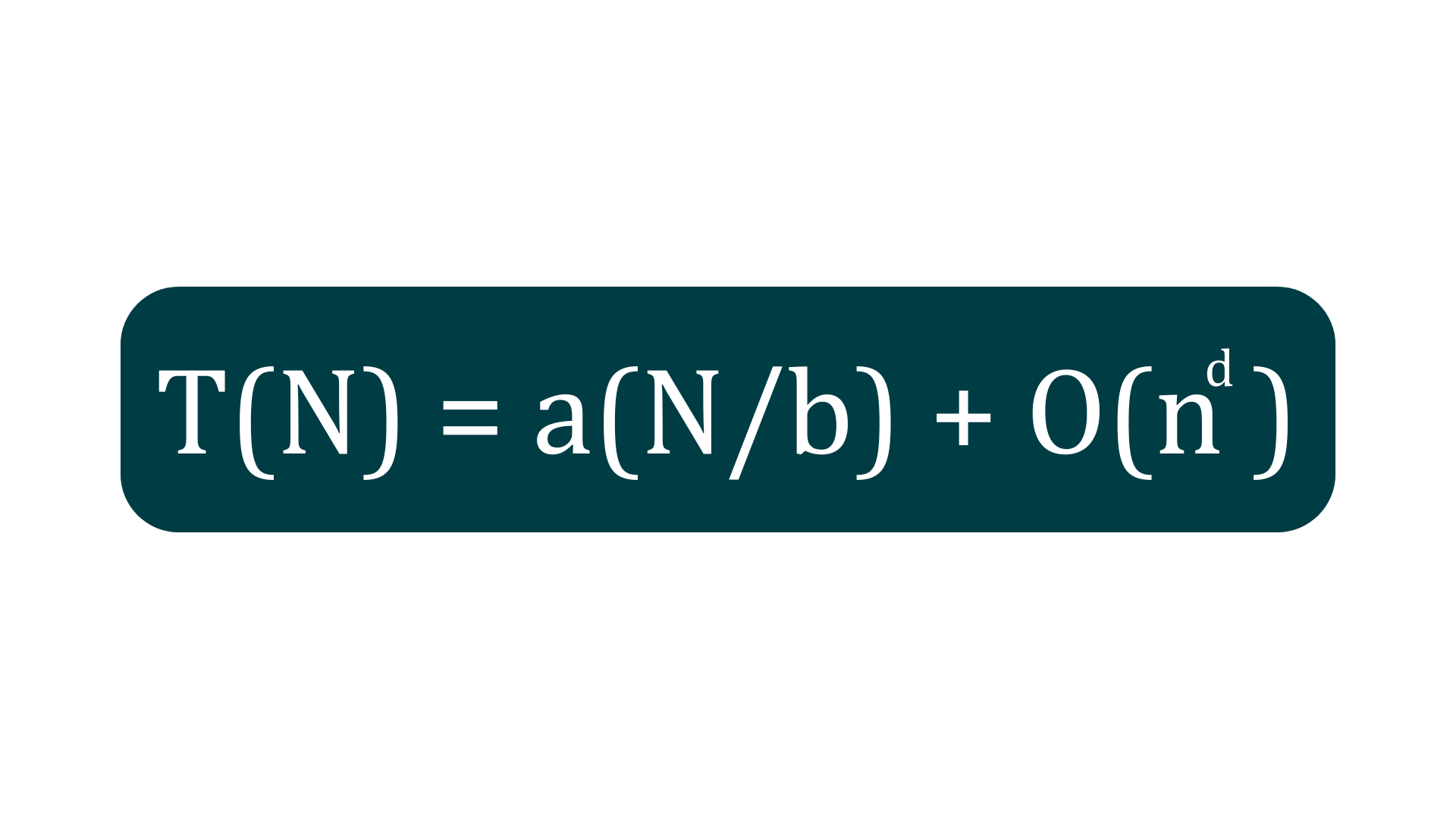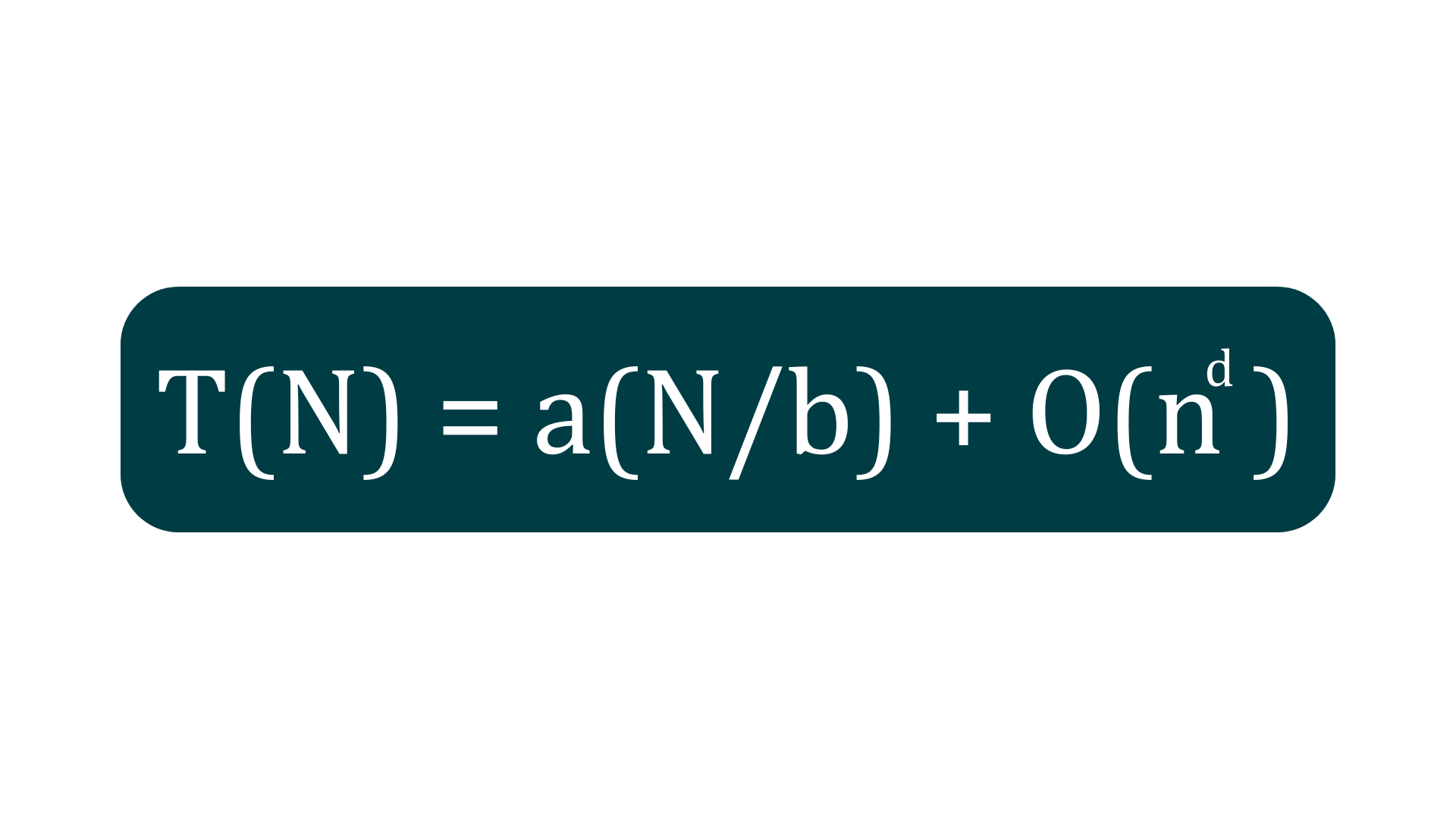The Master Theorem is used to analyze Divide-and-Conquer recurrences.

It provides a solution for recurrences of the form:

                T(n) = aT(n / b) + O(n^d)
              

Where:

• a is the number of subproblems.
• b is the factor by which the subproblem size is reduced.
• d is the exponent of the additional work done outside the recursive calls.

The solution depends on the comparison of log_b(a) and d:

• If log_b(a) > d, the complexity is O(n^log_b(a)).
• If log_b(a) = d, the complexity is O(n^d log n).
• If log_b(a) < d, the complexity is O(n^d).